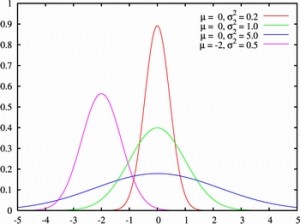
The colored lines you see in the in the graph tracing characteristic curves, are known as Gaussian, named after the German mathematician Gauss who discovered the equation (which, given it’s complexity, we might just leave at that). As you can see they are bell-shaped curves, which can be flattened or pointed. The peak, or the maximum value may not be at the center, but be moved to the beginning or the end of the curve, in this case, we are speaking of the asymmetric Gaussian. Our interest in the Gaussian is due to the fact that these curves are able to describe many natural phenomena.
For example, if we look at the horizontal line on which the curves sit, and imagine the carriages of a city underground train at a normal traffic time, we’ll see that people tend to choose the carriages according to a characteristic distribution, called the Gaussian distribution: that is, very crowded wagons in the middle, with the head and tail left rather free. Of course there are more favourable conditions that encourage the occurrence of this situation and others that may hinder it, such as the arrangement of the entries and exits of the station, the number of cars in the convoy or the number of passengers. But the statistics are consistent enough for our discussion: if people have the choice, they will never be distributed equally through all the carriages. Let’s come back to the topics most relevant to this site. Even the intensity of a gust of wind, the strength of an individual from birth to death, or of sunlight throughout the day develop this way. A Gaussian, in short, describes something that starts quietly, gradually increases, reaches a maximum, begins to decline, and then stops. The fact is that, in nature we will never find a phenomenon that appears or disappears suddenly, with a vertical ascent or descent (known in Mathmatics as a step function). The beginning and end of a something can be extremely fast (an acute Gaussian curve), but a perfectly verticle rising or falling in nature, can not exist. Maybe an engineer would explain it by saying that no phenomenon in nature can express an infinite power, a physicist would probably say that an ideal impulse does not exist in nature, a philosopher would probably talk about the cyclic constition of reality… As it is, what is important for our purposes is that whatever we do has a Gaussian trend: no matter how steeply the curve rises, or how high its peak. So, while doing physical activity (jogging, tennis, bodybuilding, chopping wood …) we see that after some initial difficulty in the first minutes, we begin to go faster (If suitable conditions are verified), but that after a time, we being to feel fatigue and our performance inevitably drops. Even our athletic performance, then, shows a Gaussian trend. Thinking about these dynamics can give us useful information to increase our efficiency (and fun) in our activities, to improve our training and keep injuries at bay. We’ll continue in the next post. Stay tuned! [Translated from Italian by Hayley Egan]
